一、正态分布假设的意义
在统计学与质量管理中,正态分布几乎无处不在。控制图、制程能力分析、t检验以及变异数分析等方法,都假设数据服从正态分布。这是因为正态分布具有对称性、可预测性,并且在大数定律和中心极限定理的支撑下具有普遍性。然而,现实世界的数据往往并不遵循正态分布。不少制程数据和可靠度数据常常偏离正态,而大部分六西格玛与制程能力分析工具却建立在正态分布的假设上。如果我们忽视了这一点,统计结果可能偏差很大,甚至导致错误决策。
二、什么是非正态分布?
非正态分布的概念指的是那些不符合正态分布特征的数据。正态分布具有几个重要特征:均值、中位数与众数相等,分布曲线呈钟形,大多数数据集中在均值附近,并符合“68-95-99.7法则”。
如果一个数据集表现出严重偏态、厚尾或多峰现象,它就很可能不是正态分布。例如,产品寿命数据往往右偏,考试成绩可能左偏,而来自不同制程的数据则可能呈现多峰。如果直接将这些数据用于Cp/Cpk计算或t检验,结果会失真。
三、如何判断数据是否正态?
判断数据是否为正态分布的方法有多种。最直观的是直方图,它能快速让人观察数据的大致形态;其次是正态概率图,如果数据点大致落在一条直线上,则可以认为数据接近正态;更严谨的是统计检验方法,包括Shapiro-Wilk检验、Kolmogorov-Smirnov检验和Anderson-Darling检验。这些方法往往借助p值进行判断,如果p值大于0.05,可以接受原假设,认为数据近似正态;如果p值小于0.05,则拒绝原假设,说明数据显著偏离正态。
四、非正态分布的应对策略
当发现数据非正态时,处理方法主要有几类。首先是调查原因,例如数据采集是否存在问题,数据是否来自不同来源,或者是否混合了不同制程的数据。其次是进行数据转换,这是在六西格玛中最常见的做法。还有一种方式是采用非参数统计方法,它们不依赖正态分布的假设。最后,如果数据确实符合某些特定分布,可以直接采用这些分布模型,比如寿命数据常用的韦布尔分布,等待时间数据常见的指数分布。在这些方法中,Box-Cox转换因其科学性和实用性,成为最常见的解决方案之一。
五、Box-Cox 转换方法
Box-Cox转换由George Box和David Cox提出,其核心思想是通过寻找一个最佳的幂次参数λ,使数据的分布尽可能接近正态。Box-Cox的公式分两种情况,当λ不等于零时,Y(λ) = (Y^λ – 1)/λ;当λ等于零时,采用对数变换ln(Y)。这里的Y必须大于零,否则无法计算。通过最大似然估计的方法,可以在λ = -5到+5的范围内寻找最优值。这个λ值的选择决定了转换的效果,例如λ=1时数据不变,λ=0时等于对数变换,λ=0.5时相当于平方根变换,λ=-1时则等同于倒数变换。Box-Cox的强大之处在于它能系统地寻找最优λ,而不是凭经验随意选择一种转换方法。
六、Box-Cox 转换案例
非正态的数据可以利用Box Cox Transformation 转化为正态的数据,这一个颇常用的方法。
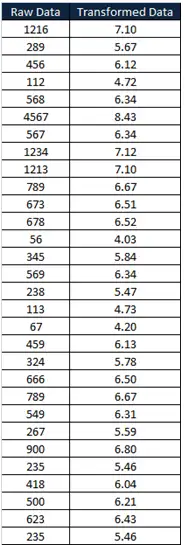
例子:原始数据:

第一步:进行正态性检验,看数据是否遵循正态分布
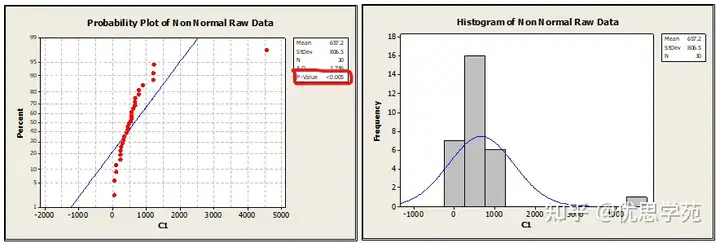
从上图中,P<0.005,因此数据不遵循正态分布,从直方图中可以明显看出数据偏向一边。
第2步:使用Box Cox变换对数据进行变换
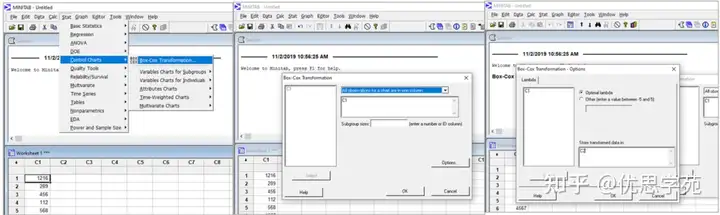
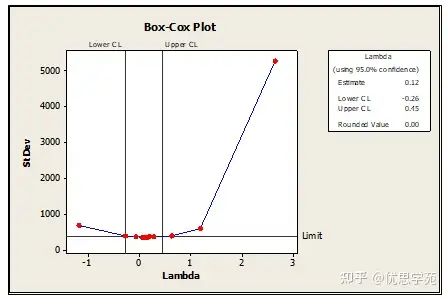
变换后的数据:
第3步:再次测试正态性
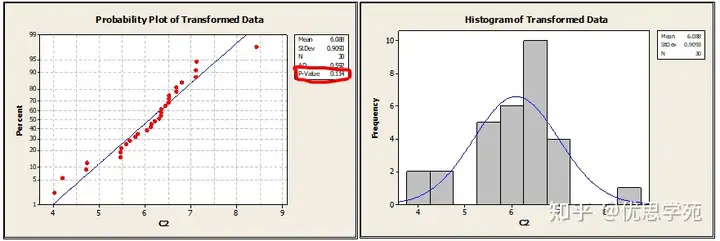
从上图中,P值>0.05,因此很明显,数据遵循正态分布,从直方图中我们也可以看到数据也是均匀分布的。由此可见,Box-Cox成功地修正了数据的偏态性。
七、Box-Cox 的局限性
Box-Cox转换并非万能。首先,它要求数据必须大于零,如果存在零值或负数,需要先进行平移处理。其次,如果数据本质上是多峰分布,例如不同生产线的数据混合在一起,Box-Cox无法解决。最后,对于极端厚尾的数据,Box-Cox的修正能力有限。因此,分析者在使用时要保持理性,不能将其当作“万能钥匙”。
八、其他常见转换方法
除了Box-Cox,还有一些常见的数据转换方法。对数变换适合右偏分布,平方根变换适合处理计数型数据,倒数变换用于右偏特别严重的情况,而Johnson转换则比Box-Cox更灵活,甚至可以处理包含零或负数的数据。不同方法各有适用范围,需要根据实际情况选择。
九、为什么六西格玛项目特别强调正态性
六西格玛之所以特别强调正态性,是因为很多核心指标建立在正态分布的基础上。Cp和Cpk是基于过程数据正态分布假设计算的,DPMO的推算依赖于正态分布尾部概率,Z值的定义本质上也是标准正态分布下的概率。如果数据严重偏态,Cp/Cpk的结果就会完全失真。举例来说,本来客户的缺陷率是千分之一,但因为数据偏态,被错误估计为百万分之一,最终导致管理层误判。因此,六西格玛黑带必须掌握如何判断正态性以及如何使用Box-Cox等方法进行修正。
十、结语:从“非正态”到“正态”,是数据分析的必修课
现实世界的数据往往不完美。作为数据分析者,不能盲目依赖统计软件的默认假设,而要主动检查数据分布,选择合适的方法。当遇到非正态数据时,首先要排除采集错误,其次可以使用Box-Cox等方法进行转换,如果转换仍不理想,则考虑采用非参数方法或者其他分布模型。只有这样,才能真正做到“用数据说话”,而不是被数据误导。
如果你想进一步深入学习六西格玛中的统计工具,理解正态分布在质量管理中的应用,建议参加优思学院的六西格玛黑带课程,在系统的训练中掌握这些知识,成为能够驾驭数据的专业人士。

