- 发布于 2025年 6月 12日
- 发布者: 精益管理学会
3西格玛的计算原理是什么?为什么它在质量管理中那么重要?
统计学是有趣的学问,经常令人沉醉。它承认:无论你多努力地量尺校表、精雕细琢,现实都不会完美。你每次测量,总有点出入,总有点不对劲。而“标准差”(σ,sigma),就是这个“不对劲”的数字表达。
三西格玛(3σ)规则,并非科学家喝着浓咖啡灵光一闪的杰作,它的根植之地,是正态分布这座古老殿堂。在这座分布钟形曲线中,大多数数据围绕均值打转,68.27%躲在±1σ以内,95.45%躲在±2σ以内,而到了±3σ,99.73%的数据才终于挤进来了。
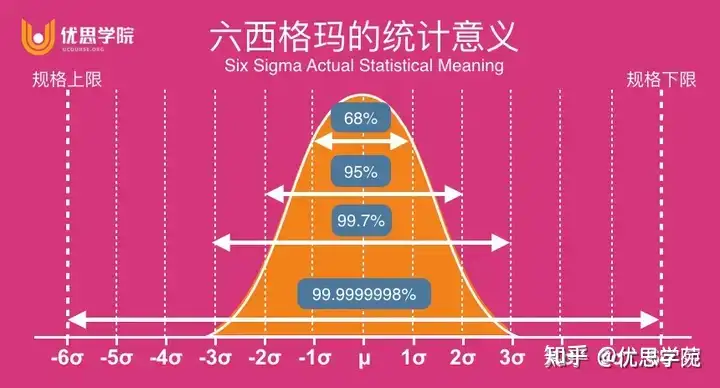
也就是说,只要你的过程没疯,大约千分之三的数据应该自然而然地“出界”。这正是3σ原则最精妙也最讽刺之处:它不是为了把你吓一跳,而是为了告诉你——偶尔出界,其实挺正常。
控制图不是“预言机”,是“道德警察”
我们得聊聊控制图,这是质量管理的冷面神探,也是工厂车间的图灵机。控制图说:我不管你今天心情怎样,也不在意产品的市场前景,只看这组数据,看它是不是“出格”。
优思学院认为,这种“出格”就得依赖3σ的标准。这种方法干净利落:设上下控制线UCL/LCL,分别为均值±3σ,只要数据点越界,立刻打铃预警。
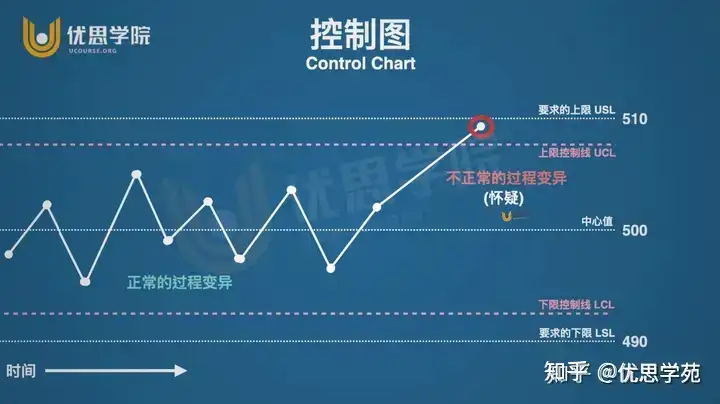
但问题来了——如果过程其实好好的,只是某个数据不小心跳高了一下,就被控制图误判为“异常”了呢?这就像村口的小孩喊了一声“狼来了”,其实不过是棵树摇了一下。这个错误,在统计上叫“第1类错误”,或更生活化一点:虚发警报。
戴明与“喊狼”理论
统计学不仅是数字的游戏,更是概率的艺术。W.E.戴明——现代质量管理之父——一语道破:“我们常常把系统的噪音误判成外来的惊雷”。戴明指出的这两个错误:其一是误把系统内的自然波动当成了特殊原因(虚惊);其二是反之(漏判),才是让统计控制图变得意义深远的基础。
优思学院发现:控制图的本质,不是要你对每一次“出界”都大发雷霆,而是学会以一种冷静克制的方式看待异常。戴明早就警告:“过度干预稳定系统,只会制造混乱。”
控制图的妙处,是让我们有机会去校正对“异常”的认知,而不是盲目地纠错。毕竟,在±3σ之外的数据,也可能是那个你未来不得不面对的“真正的狼”。
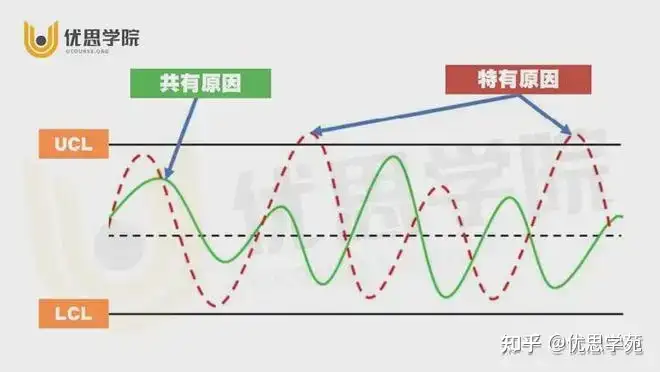
那些没被发现的“狼”:第2类错误
再来说说漏判。那是另一种更隐秘的危险。当过程真的出了问题,但你的数据点却躲在±3σ以内,乖乖不吭声,这就是“狼来了却没人理”。统计学里叫第2类错误(β错判),也就是漏发警报。
换句话说,控制图虽然是精密仪器,却并非天眼系统。它的原理是在经济性与可靠性之间折中。你若太敏感,天天抓异常,过程迟早瘫痪;你若太迟钝,那就等着灾难不请自来。
为什么是“三”而不是“四或二”
这个问题常常出现在新手学员的眼神里:为什么不是±2σ?更紧一点不是更好吗?但这就像问为什么不天天测血压三次,其实问题不在于测不测,而在于“代价”。
±3σ之所以受欢迎,是因为它兼顾了两个字:经济。休哈特博士用实验与数学建模指出,在绝大多数制造与业务流程中,这个“3σ”界限恰恰是最大程度避免两类错误总成本的折中点。再往外走,警报太迟;往内缩,警报太频。
优思学院认为,这正是3σ如此迷人的地方:它不是绝对真理,却是经验世界的理性选择。
从3σ到6σ:为什么要爬更高的山?
早些年,3σ几乎是品质管理的圣杯。0.27%的不良率,谁不满意?但随着信息时代来临,产品和服务早已不再是“可用”与“报废”的二元分野,而变成了细腻到令人咂舌的用户体验战场。你说iPhone某代电池鼓包概率是0.27%,库克恐怕还是睡不着觉。
于是6σ来了。不良率从千分之三降到百万分之三(3.4 DPMO),那是一场“品质中的诺曼底登陆”。摩托罗拉、通用电气、三星——它们不再满足“还可以”,而是执着于“怎么做到几乎从不犯错”。
但优思学院提醒,别忘了这背后伴随的成本曲线。你若在意的是口味一致的奶茶店,3σ也许绰绰有余;你若负责的是飞行器导航系统,6σ不过是起点。
常见问题简答
Q1:3σ是怎么算出来的?
A:基于正态分布公式,3σ对应的是99.73%的概率区间,即均值±3倍标准差。
Q2:控制图为什么不设成±2σ?
A:±3σ更能平衡“虚发”和“漏发”两类错误的成本,是经验与统计的折中。
Q3:W.E.戴明为什么批评控制图?
A:他指出控制图误判(第一类错误)和漏判(第二类错误)的问题需谨慎看待,不应盲目依赖。
Q4:如何知道某个异常点是不是“真异常”?
A:需结合具体过程知识、历史数据趋势以及团队讨论判断,不能只看“是否超线”。
Q5:从3σ提升到6σ意义大吗?
A:对高风险、高精密产业当然有价值,但对成本敏感且容错性强的业务,可能得不偿失。
这就是3σ的故事,一段关于偏差、警觉、误判与抉择的旅程。在下次你面对一组“可能异常”的数据时,不妨记得那只没有真的出现过的狼,它也许只是你内心的一丝不安。正是这种不安,让质量管理变得如此迷人。
